🔥 Scaling Predictive Coding to 100+ Layer Networks

📖 TL;DR: We introduce \(\mu\)PC, a reparameterisation of predictive coding networks that enables stable training of 100+ layer ResNets on simple tasks with zero-shot hyperparameter transfer.

μPC enables stable training of 100+ layer ResNets with zero-shot learning rate transfer. (Right) Test accuracy of ReLU ResNets with depths H = {8, 16, 32, 64, 128} trained to classify MNIST for one epoch with standard PC, μPC and BP with Depth-μP. (Left) Example of zero-shot transfer of the weight and activity learning rates from 16- to 128-layer Tanh networks.

This post briefly explains my recent paper \(\mu\)PC: Scaling Predictive Coding to 100+ Layer Networks. For the first time, we show that very deep (100+) layer networks can be trained reliably with a local learning algorithm. To do this, we basically marry predictive coding (PC) with the “maximal update parameterisation” (\(\mu\)P) [1].

Background

For a brief review of PC, see my previous posts here and here. See also this video by Artem Kirsanov for a beautiful visual explanation of PC. In one sentence, PC networks have an energy function which is a sum of many local energies (as opposed to a global loss), and are trained by minimising this energy with respect to both activities and weights.

\(\mu\)P is essentially a theory that tells you how to scale your network such that the learning dynamics are stable across different model sizes such as width and depth [1]. See my previous post for a quick review.

Problems with standard PC

In the paper we expose two main problems that arise when training standard PC networks (PCNs) at large scale:

1. the inference landscape becomes increasingly ill-conditioned with model size (particularly depth) as well as training time; and
2. the forward pass tends to vanish/explode with depth.

The second problem is shared with backpropagation-trained networks, while the first is unique to PC (and possibly other energy-based algorithms). Together, they make training and convergence of the PC inference dynamics challenging, especially at large depth.

To make a long story short, we find that it seems impossible to solve both problems at once, but because PCNs with highly ill-conditioned inference landscapes can still be trained, we aimed to solve the problem (2) at the expense of problem (1).

\(\mu\)PC

We reparameterise PCNs using the recent Depth-\(\mu\)P parameterisation [2][3], which basically ensures that the forward pass is stable independent of width and depth for residual networks (solving problem (2) above). We call this reparameterisation “\(\mu\)PC”. In practice, this just means applying the Depth-\(\mu\)P scalings to the PC energy function. See the paper for more details.

Remarkably, we find that \(\mu\)PC allows stable training of 100+ layer networks on simple classification tasks with competitive performance and little tuning compared to current benchmarks. This result holds across different activation functions.

What’s more, \(\mu\)PC enables zero-shot transfer of both weight and activity learning rates across model widths and depths, consistent with previous results with Depth-\(\mu\)P [2][3]. This means that you can tune a small model and then transfer the optimal learning rates to a bigger (wider and/or deeper) model, avoiding the expensive cost of tuning at large scale [4].

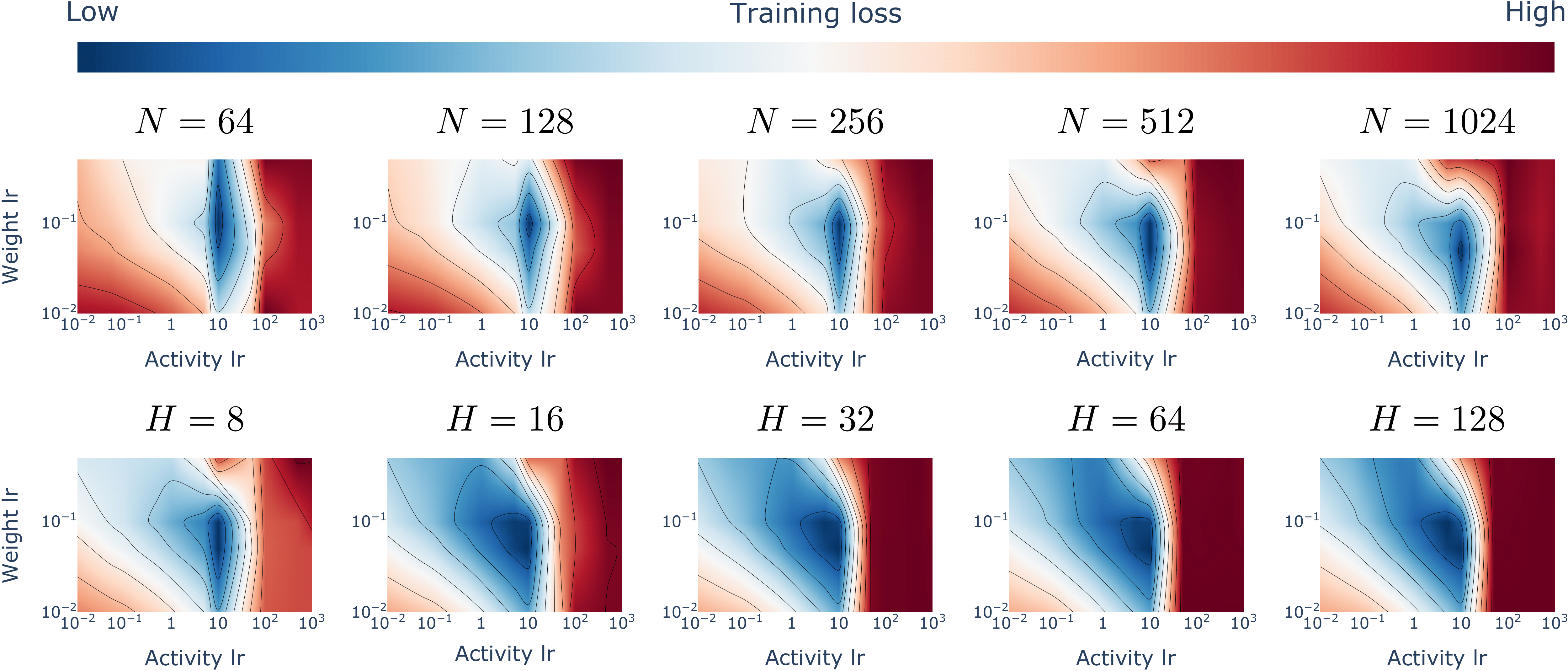μPC enables zero-shot transfer of the weight and activity learning rates across model widths N and depths H. Minimum training loss achieved by ResNets of varying width and depth trained with μPC on MNIST across different weight and activity learning rates.

Limitations and future directions

While we scaled model size to unprecendented levels, the main limitation of this work remains the simple datasets tested (with the camera-ready version including experiments with CIFAR10). This was mainly because of the high compute cost of running the PC inference dynamics to equilibrium at such scale. For this reason, I am convinced that research on similar energy-based algorithms needs to be tighly integrated with hardware design, if we are to achieve true breakthroughs.

It also remains to be seen whether transformers (or equally expressive architectures), shallow or deep, can be trained at all with PC. Fortunately, both convolutional and transformer-based architectures admit Depth-\(\mu\)P parameterisations [1][3].

It would also be useful to better understand \(\mu\)PC theoretically, for example why it works despite not solving the ill-conditioning of the inference landscape with depth (problem 1 above). This could lead to an even better parameterisation of PCNs.

Finally, part of our analysis applies to other inference-based algorithms, and it would be interesting to see whether these algorithms could also benefit from \(\mu\)P-like parameterisations.

\(\mu\)PC is made available as part our JAX library for PCNs [5], along with an example notebook. For more details, see the paper.

References

[1] Yang, G., & Hu, E. J. (2021). Tensor programs iv: Feature learning in infinite-width neural networks. In International Conference on Machine Learning (pp. 11727-11737). PMLR.

[2] Yang, G., Yu, D., Zhu, C., & Hayou, S. (2023). Tensor programs vi: Feature learning in infinite-depth neural networks. arXiv preprint arXiv:2310.02244.

[3] Bordelon, B., Noci, L., Li, M. B., Hanin, B., & Pehlevan, C. (2023). Depthwise hyperparameter transfer in residual networks: Dynamics and scaling limit. arXiv preprint arXiv:2309.16620.

[4] Yang, G., Hu, E., Babuschkin, I., Sidor, S., Liu, X., Farhi, D., ... & Gao, J. (2021). Tuning large neural networks via zero-shot hyperparameter transfer. Advances in Neural Information Processing Systems, 34, 17084-17097.

[5] Innocenti, F., Kinghorn, P., Yun-Farmbrough, W., Varona, M. D. L., Singh, R., & Buckley, C. L. (2024). JPC: Flexible Inference for Predictive Coding Networks in JAX. arXiv preprint arXiv:2412.03676.